题目分析
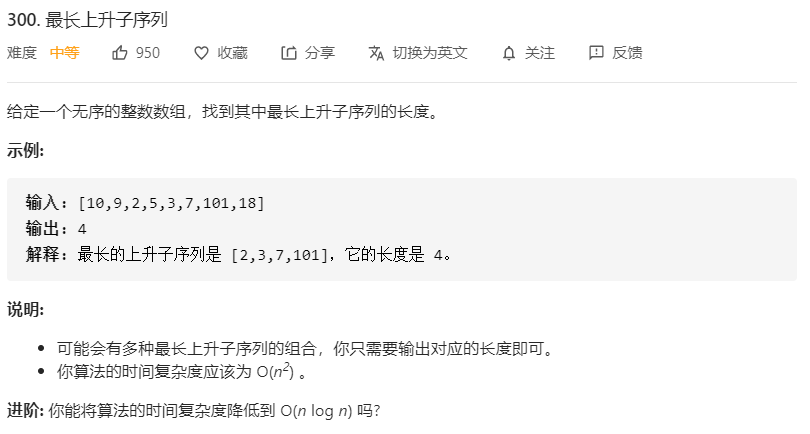
最长上升子序列(Longest Increasing Subsequence, LIS):这是非常有趣的一个题目,也是笔试面试常常出现的一道数组题,这道题目小伙伴们必须要掌握动态规划的解法,但是能否想到更加巧妙的方法呢?
DP
我们使用动态规划进行求解,dp[i]表示右端点选择第i个数可得的最长上升子序列,可以得到状态转移方程
$$ dp[i] = \max_{j = 1}^{i - 1} dp[j] + 1 \ \ \ \ \ \ \ (if \ \ \ nums[i] > nums[j]) $$
当考虑到所有情况后,就可以得到右端点为任何情况下的最大值,然后求dp数组的最大值即可。DP的时间复杂度为$O(n^2)$,空间复杂度为$O(n)$。
1 | class Solution(object): |
贪心+二分查找
我们思考一些可能出现的情况,假设前k个元素的最长上升子序列为[1, 3, 5, 7, 9]。
- **如果第k + 1个元素大于9,假设为11,则最长上升子序列变为[1, 3, 5, 7, 9, 11]**。
- 如果第k + 1个元素小于9,假设为6,最长上升子序列长度不变,但是会将大于6的最小值变为6,则此时最长上升子序列变为[1, 3, 5, 6, 9],当以后再出现7时,最长上升子序列的长度仍然不变,但是子序列就已经更新为更好的一组值了[1, 3, 5, 6, 7]。
也就是说当后续出现更小的值时,不会立刻改变最长子序列的长度,而是从中间的某个地方开始逐渐替换,当此时出现更大的数字时,仍然按照替换之前的子序列继续追加。如果此时出现较小的数字时,则继续替换。当替换到最后一个数字时,说明子序列已经出现了更优解,以后按照更优解进行计算。
从上升子序列中寻找大于某个值的最小值时,可以使用二分查找法,这样可以将第二次遍历的时间复杂度大大缩小。算法的时间复杂度为O(nlog(n)),空间复杂度为O(n)。
1 | class Solution(object): |
树状数组
这是我在2022年9月重新写这道题时查看其他人的题解发现树状数组的方法,我是完全没有想到的,往这个思路去想,也很难想到。这里不考验大家了,直接分享这种思路吧。
我们从DP的做法开始思考,我们让dp[x]表示以元素x结尾的上升子序列长度,注意这里并非是下标x。
因此有下列公式
$$ dp[x] = \max_{y < x} dp[y] + 1 $$
所以本题可以转化为求从dp[0]到dp[x - 1]的元素最小值,且dp[x]的值可能会动态修改。
是不是和Leetcode307题很类似,前缀和的题目可能会动态修改arr[i],且会计算arr的前缀和。
前缀和的题目可以使用树状数组和线段树优化到O(nlog(n),我们也试一下能否利用这种方式求解。
这里使用树状数组和前缀和有一个技巧,就是将数据进行压缩,因为数据的范围是[-10000, 10000],但是数组的长度只有2500以内,因此可能存在重复或者稀疏数组。
举个例子,[1,6,20,100]等价于[1,2,3,4],因此可以将原数组进行压缩。我们也要学会这里的压缩方式。
算法的时间复杂度为O(nlog(n)),空间复杂度为O(n)。
1 | class Solution { |
线段树
线段树没啥好说的,可以参考线段树相关的博客。
能使用树状数组求解的问题,基本上都可以使用线段树解决。
下面直接给出代码,小伙伴们可以参考线段树的博客先看明白模板,然后做一些微调即可。
算法的时间复杂度为O(nlog(n)),空间复杂度为O(n)。
1 | class Solution { |
刷题总结
这个题目虽然动态规划是必须要掌握的,但是贪心+二分的思路也是非常非常重要的,因为一旦笔试面试中出现这个问题,往往不是考察动态规划的知识点。笔试中会给很大的数据量,面试时面试官也会问有没有更好的解法,所以小伙伴们一定要学会它。